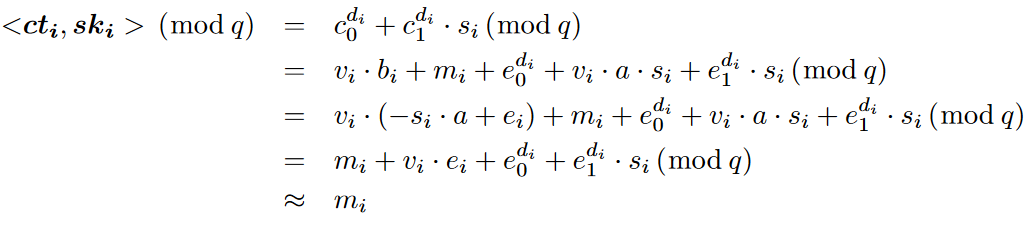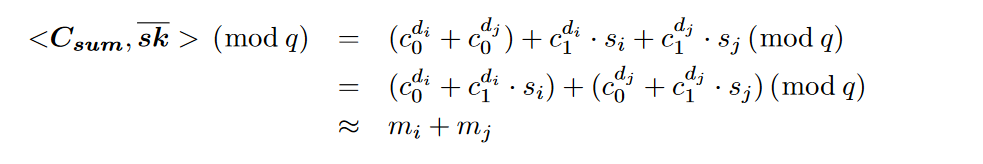MK-CKKS

1 MK-CKKS

是一种基于错误环学习 (RLWE) 的同态加密方案。

$R=\mathbb{Z}[X]/(X^n+1)$ $R$是分圆环，$n$是2的幂次，$\mathbb{Z}[X]$是整数系数的多项式环，$R$中的元素满足$X^n=-1$。$\:R_{q}=\mathbb{Z}_{q}[X]/(X^{n}+1)\:$是 $R$ 的残差环¹，其系数以整数 $q$ 为模。（$R_q=\mathbb{Z}_q[X]/(X^n+1)$ 表示模 $q$ 的多项式环 $\mathbb{Z}_q[X]$ 通过关于多项式 $X^n+1$的同余关系构造出的一个剩余类环。)

对于参数 $(n,q,\chi,\psi)$，我们的 RLWE 假设是，给定形式为 $\:(a,b=s\cdot a+e)\in R_q^2\text{,}\:$的多项式，当从 $R_q$ 中均匀随机选择 $a$ 时，项$b$ 在计算上无法与 $R_q$ 的均匀随机元素区分开来，$s$ 从 $R_q$上的密钥分布$\chi$ 中选择，$e$ 从 $R$ 上的C错误分布 $\psi$ 中抽取的 。

我们用粗体表示向量，并使用$\langle\mathbf{u},\mathbf{v}\rangle$ 表示两个向量 u 和 v 的点积。$x\leftarrow\Gamma\text{}$表示根据分布 Γ 对 x 进行采样。λ 表示整篇论文的安全参数。$g\in Z^{d}\quad\text{}$是一个积分向量，called the gadget vector。MK-CKKS 假定公共参考字符串 (CRS) 模型，因此所有设备共享一个随机多项式向量 $\mathbf{a}\leftarrow U(R_{q}^{d})$，这里 U (·) 表示均匀分布。设$\textit{sk}_\mathbf{i}=(1,s_i)$ 作为密钥 $s_i$，$\overline{\mathbf{sk}}=(1,s_{1},...s_{N})$用于连接多个密钥。$\mathbf{c t_i}=(c_0^{d_i},c_1^{d_i})$是明文$m_i$的密文来自远程设备 $\ d_i$，$\text{}i=1,\ldots,N$

2 设置

对于给定的安全参数 $\lambda$，设置 RLWE 维数 $n$、密文模数 $q$、密钥分布 $\begin{array}{c}\chi\end{array}$ 和误差分布$\psi$ 在 $R$上。生成一个随机向量。返回公共参数$(n,q,\chi,\psi)$。远程设备 $d_{i}$生成其秘密密钥 $\:s_{i}\leftarrow\chi\:$，并计算其公钥为 $\mathbf{b_{i}}=-s_{i}\cdot\mathbf{a}+\mathbf{e_{i}}\in R_{q}^{2}$，此处 $\mathbf{e}_{i}$是从 $R$ 上的误差分布 $\psi$ 中得出的误差向量。

3 编码和解码

在加密之前，首先将一个复数展开为一个向量，复数规范嵌入映射将其编码为环R的多项式。解码将解密后的多项式转换为复数向量。

4 加密

将消息向量编码为明文 $m_i$（即分圆环的元素）后，$d_i$ 将 $m_i$加密为密文 $\mathbf{c t_i}=(c_0^{d_i},c_1^{d_i})$其中$\:c_0^{d_i}=v_i\cdot b_i+m_i+e_0^{d_i}\:(\mathrm{mod}\:q)\:$ 和$c_{1}^{d_{i}}=v_{i}\cdot a+e_{1}^{d_{i}}\:(\mathrm{mod}\:q)$。这里$\ a=\mathbf a\text{}[0]\:$ 和 $\ b_i=\textbf{b}_i[0]$,$\:v_{i}\leftarrow\chi\:$ 和 $e_{0}^{d_{i}},e_{1}^{d_{i}}\leftarrow\psi$。插入小错误以确保安全，并且可以在执行同态操作后通过舍入操作将其删除。在 MK-CKKS 中，与 N 个不同方相关联的附加密文的形式为$\mathbf{C}_{\mathrm{sum}}\stackrel{\mathrm{def}}=\left(\sum_{i=1}^{N}c_{0}^{d_{i}},c_{1}^{d_{1}},c_{1}^{d_{2}},\ldots,c_{1}^{d_{N}}\right)\in R_{q}^{N+1}$

Decryption of individual ciphertext. $d_i$ 计算$\textit{sk}_\mathbf{i}=(1,s_i)$和 $\mathbf{c t_i}=(c_0^{d_i},c_1^{d_i})$的点积，如下所示

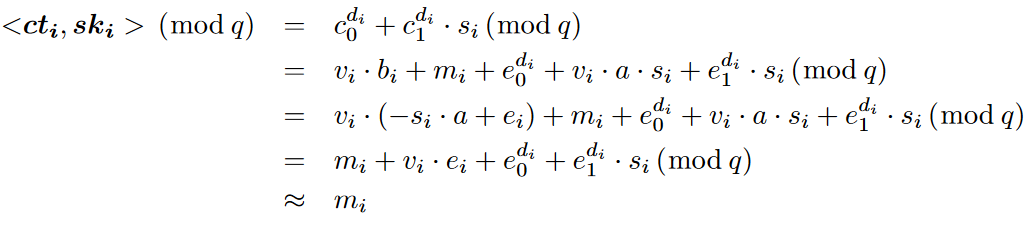
5 加法同态

设$\mathbf{c t_i}=(c_0^{d_i},c_1^{d_i})$ 和$\mathbf{c t_j}=(c_0^{d_j},c_1^{d_j})$ 是来自远程设备 $d_i$ 和 $d_j$ 的明文消息 $m_i$ 和 $m_j$ 的两个密文。密文的总和是$\mathbf{C}_{\mathrm{sum}}\stackrel{\mathrm{def}}=(c_{0}^{d_{i}}+c_{0}^{d_{j}},c_{1}^{d_{i}},c_{1}^{d_{j}})$它可以通过计算 $C_{s u m}$ 和$\overline{\mathbf{s k}}=(1,s_{i},s_{j})$ 的点积来解密。正确性证明如下：

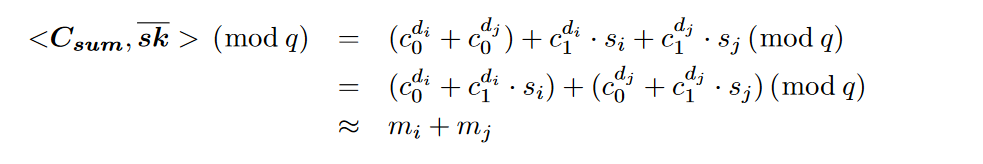
6 解密总和

MK-CKKS 中引入了基于噪声泛洪的分布式解密，因为假设任何一方都持有多个密钥是不合理的。解密包括两种算法：部分解密和合并。

¹. 残差环（Residue Ring）是一个环的剩余类环。给定一个环 $R$ 和一个理想 $I$，则 $I$ 中的每个元素 $a$ 都可以对 $R$ 中的每个元素取模得到一个剩余类 $[a]$。所有这些剩余类构成一个新的环，称为 $R$ 对 $I$ 的剩余类环，记作 $R/I$。具体来说，$R/I$ 中的元素是形如 $[a]$ 的剩余类，其中 $a\in R$ 且 $[a]=[b]$ 当且仅当 $a-b\in I$。$R/I$ 中的加法和乘法运算分别定义为： $[a]+[b]=[a+b]$ $[a]\cdot[b]=[ab]$在密码学中，残差环常被用于构造离散对数问题，从而实现公钥密码学中的加密和签名算法，如 Diffie-Hellman 密钥交换、ElGamal 加密、DSS 签名等。常用的残差环包括模素数的剩余类环 $\mathbb{Z}/p\mathbb{Z}$，以及模多项式的剩余类环 $R_q=\mathbb{Z}_q[X]/(f(X))$，其中 $f(X)$ 是一个不可约多项式 ↩